I recently received a question in regards to the thermistor formula found on one of the SATL build posts asking how I came about the variables used in the thermistor formula. The thermistor formula and variables I used can be found on the Arduino Playground however it made me think if the formula being used was accurate for the Vishay 10K thermistor I was using.
Below we have the Thermistor function in question in which it converts the ADC value to a resistance value in ohms, applies a formula and convert the result to celsius.
double Thermistor(int RawADC) {
double Temp;
Temp = log(((10240000/RawADC) - 10000)); // Minus by 10K as that's the resistor in series with the thermistor
Temp = 1 / (0.001129148 + (0.000234125 * Temp) + (0.0000000876741 * Temp * Temp * Temp));
Temp = Temp - 273.15; // Convert Kelvin to Celcius
return Temp;
}
Steinhart–Hart equation
The formula used is called the Steinhart–Hart equation which models resistance to temperature, there is the “full version” and the “commonly used” one. A, B, C and D in the functions below are called the coefficients.
Full version: 1/T= A + B*ln(R/Rt) + C*ln(R/Rt)2 + D*ln(R/Rt)3
Commonly used: 1/T= A + B*ln(R/Rt) + D*ln(R/Rt)3
You’ll notice the “C*ln(R/Rt)2” part is removed, according to Wikipedia it’s the reason is: “because it is typically much smaller than the other coefficients, and is therefore not shown above”. The thermistor function above uses the “commonly used” formula.
You might see that there is an inconsistency between the thermistor function code and the Steinhart–Hart equation; it’s that we do a natural logarithm of thermistor’s resistance in ohms whilst in the equation we do the natural logarithm of the thermistor’s resistance divided by the thermistor’s resistance at 25C. This inconsistency is solved by reducing the A coefficient which we will confirm later on. Also be aware that using the Windows calculator log function will actually do the base10 logarithm which isn’t the same as the natural logarithm.
Reading the datasheet
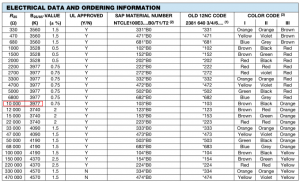
Let’s bring up the Vishay thermistor datasheet and see if we can find any values for the coefficients. On page 4 we can see some formulas and a table with the coefficients, the ones with the positive K in brackets are used to find resistance and the negative K are used to find temperature. We’ll need to find which line in the table to use.
On page 2 it maps the thermistor resistance at 25C (R25) to the B25/85 value, for a 10K thermistor it’s 3977.
Now we know which coefficients we need to use – line number 9. Instead of doing the math ourselves, as with everything ‘there’s a calculator for that’ – Steinhart-Hart Thermistor Calculator.
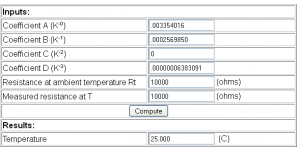
Calculations
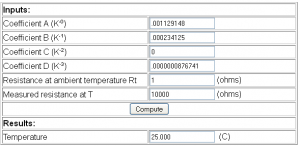
We fill in the A, B and D coefficients (we ignore C as mentioned before) and we try at 10K ohms for the T value and the thermistor value at 25C (Rt) in which we receive the result 25C as expected, this means our coefficients (well actually just the A coefficient because the results from B*ln(Rd/Rt) work out to be 0, same goes for D) seem to be correct.
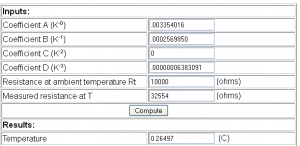
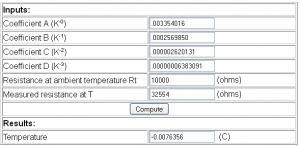
Now we’ll try the thermistor resistance being 32554 ohms which corresponds to being 0C degrees (page 10).
Our coefficients appear to be functioning correctly, it reads 0.26497C which is close. However what if we want it even more close to 0C?
We’ll use the “full version” of the Steinhart–Hart equation this time by filling in the C coefficient. This time it reads -0.0076356C which is closer than before, so we should use the “full version”.
Analyse the existing Thermistor function
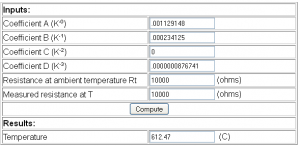
Let’s analyse the existing thermistor function by entering the coefficients into the calculator. We’ll start with 10K ohms as Rt and T. The existing function does a log of 10,000 which gives us 9.2103 which is different to the log of 1 (10,000/10,000) gives us 0 which the calculator was doing for us.
It gives us 612.47C. Let’s change Rt from 10,000 to 1 as that’s the main difference, this would be like saying log (10,000/1) which mimics the existing thermistor function.
Ah that gives us the results we need. Apart from the log differences, the other difference is in the A coefficient: 0.001129148 vs 0.00354016 (Vishay) which leads me to believe that using it is like dividing by 10,000. So let’s make some changes to the function so that it follows the Steinhart–Hart equation exactly and we’ll use the “full version” as it seems to give us greater accuracy.
New thermistor function
double thermistorTemp (int RawADC) {
double Temp;
Temp = log((double)((10240000/RawADC) – 10000) / 10000); // We divide by our thermistor's resistance at 25C, in this case 10K
Temp = 1 / (0.003354016 + (0.0002569850 * Temp) + (0.000002620131 * Temp * Temp)+ (0.00000006383091 * Temp * Temp * Temp));
Temp = Temp – 273.15; // Convert Kelvin to Celsius
return Temp;
}
We now divide the thermistor resistance by 10,000 assuming that the user is using a 10K thermistor and substitute the Vishay coefficient values including the C coefficient.
Results
| Temperature | Old Thermistor function | New Thermistor function |
|---|---|---|
| -40C | -39.820 | -40.000 |
| -25C | -24.869 | -25.010 |
| 0C | 0.057915 | -0.0076356 |
| 50C | 49.971 | 50.006 |
| 80C | 80.002 | 80.011 |
| 100C | 100.06 | 99.998 |
| 125C | 125.21 | 125.00 |
| 150C | 150.46 | 150.01 |
The further you move away from 25C in either direction, the higher the difference between the old thermistor function and our new one however it’s not by very much at all which means the existing thermistor function is still viable to use.
Tolerance
The last part and probably the most important for accurate temperature reading is the tolerance of the thermistor, you can find some 0.5%, 1%, 2%, 3%, 5% and even 10%.
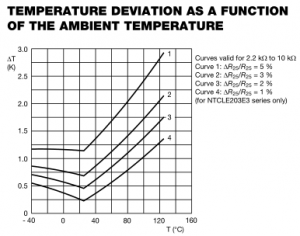
Vishay’s datasheet (page 2) shows us how much deviation in temperature (plus or minus) depending on the tolerance. If we used a 5% tolerance part, at 0C the deviation would be about 1.2C so the thermistor might read between -1.2C to 1.2C. It gets a bit worst at higher temperatures as you can see, for 80C the deviation is 2C, it might be between 78C to 82C.
Conclusion
It turns out that the existing thermistor function’s accuracy was very close to the new thermistor function we wrote. By re-writing the thermistor function to follow the Steinhart–Hart equation exactly we can now simply change the coefficients/thermistor value more easily now and by substituting our Vishay’s thermistor’s coefficients we can have slightly better temperature readings.







Hello I’m trying to do it with a thermistor of 50k. My question is, if I need to change the values from [log(((10240000/RawADC) – 10000))] because I changed 10000 and I put 50000 and I did not get the accurate temperature. The information of my sensor is R25=50K B=3950 and the values from the tables are A=0.003354016 B=0.0002460382 D=0.0000001034240. Thank you for your help.
Hi Hector,
If you are using the “old thermistor” function, the 10K is built into the later parts of the equation which is why it’s hard to change thermistor values. If you use my “new thermistor” function, you can just replace the divide by 10K thermistor to divide by 50K thermistor.
Did this work for the 50k thermistor with those values? I am not able to achieve accurate readings.
Hector, could you post your code for the 50k thermistor?
For 50K thermistor:
double thermistorTemp (int RawADC) {
double Temp;
Temp = log((double)((51200000/RawADC) – 50000) / 50000); // We divide by our thermistor’s resistance at 25C, in this case 50K
Temp = 1 / (0.003354016 + (0.0002569850 * Temp) + (0.000002620131 * Temp * Temp)+ (0.00000006383091 * Temp * Temp * Temp));
Temp = Temp – 273.15; // Convert Kelvin to Celsius
return Temp;
}